Get started with MAX Graph in Mojo

Ehsan M. Kermani

Developer Relations

Updated: Jul 2, 2024 |

32 min read

mojo

graph

MAX Engine is a next-generation compiler and runtime library for running AI inference. With support for PyTorch (TorchScript), ONNX, and native Mojo models, it delivers low-latency, high-throughput inference on a wide range of hardware to accelerate your entire AI workload. As highlighted in the recent MAX version 24.3 release, the MAX platform enables users to fully leverage the capabilities of the MAX Engine by creating bespoke inference models using the MAX Graph APIs. The Graph API offers a low-level programming interface for constructing high-performance symbolic computation graphs in Mojo. This interface provides a uniform representation of symbolic values and a suite of operators that process these symbols to construct the entire graph.

In this tutorial, we guide you step-by-step how to use the MAX Graph API. In a nutshell, working with MAX Graph API involves three main steps:

1. Building and verifying the graph.
2. Creating an inference session and compiling the graph.
3. Executing the graph with input(s) and retrieving the output(s).

We begin by creating two straightforward graphs for addition and matrix multiplication in Mojo, demonstrating how to compile and execute these graphs. Then we proceed to implement a two-layer feedforward neural network with ReLU activation for inference on MNIST data, comparing the accuracy to a PyTorch implementation.

Create a virtual environment

Using a virtual environment ensures that you have the MAX and Mojo version that's compatible with this project. We'll use the Magic CLI to create the environment and install the required packages.

You can install Magic on macOS and Ubuntu Linux with this command:

curl -ssL https://magic.modular.com/ | bash

curl -ssL https://magic.modular.com/ | bash

Then run the source command that's printed in your terminal.

1. Start by cloning the nightly branch of the MAX GitHub repository

   git clone -b nightly https://github.com/modularml/max/
   cd max/tutorials/max-graph-api

   git clone -b nightly https://github.com/modularml/max/
   cd max/tutorials/max-graph-api

2. You can check your Mojo version like this:

   magic run mojo --version

   magic run mojo --version

   mojo 2024.8.2715 (fe1c27f0)

   mojo 2024.8.2715 (fe1c27f0)

If you're new to the Mojo language, you can learn the basics in the Introduction to Mojo.

If you have any questions along the way, ask them in our Discord server. Should you encounter any issues, we recommend checking the known issues first.

Build a "Hello, world!" graph

To begin familiarizing ourselves with the Graph API, we start by constructing a simple addition graph. We will verify and compile this graph, and then proceed to execute it.

Below is a straightforward graph that takes two inputs; input0 and input1. It adds these inputs together and produces output0 as the output.

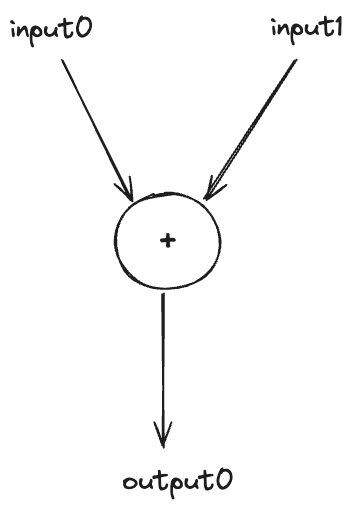
1. Build the graph

To construct the addition graph, we start by importing the necessary modules. We then instantiate the Graph by specifying two input types of fixed static dimension 1 (we will later see other types of supported dimensions such as symbolic dimension). Next, we create a symbolic representation of the addition with the expression out = graph[0] + graph[1]. Here graph[0] refers to the first input input0 and graph[1] to input1. This operation adds two inputs together. Finally, we designate out as the output of the graph by calling graph.output(out).

from max.graph import Graph, TensorType, Type

graph = Graph(in_types=List[Type](TensorType(DType.float32, 1), TensorType(DType.float32, 1)))
out = graph[0] + graph[1]
graph.output(out)
print(graph)

from max.graph import Graph, TensorType, Type

graph = Graph(in_types=List[Type](TensorType(DType.float32, 1), TensorType(DType.float32, 1)))
out = graph[0] + graph[1]
graph.output(out)
print(graph)

We can print the graph to visually confirm its structure. The output should show the following representation where rmo and mo are Modular's internal intermediate representations

%0 = rmo.add(%arg0, %arg1) : !mo.tensor<[1], f32>, !mo.tensor<[1], f32>

%0 = rmo.add(%arg0, %arg1) : !mo.tensor<[1], f32>, !mo.tensor<[1], f32>

This line corresponds to the symbolic addition operation out = graph[0] + graph[1].

The subsequent line

mo.output %0 : !mo.tensor<[1], f32>

mo.output %0 : !mo.tensor<[1], f32>

indicates that %0 has been set as the output of the graph, aligning with the graph.output(out) in our code.

The complete graph representation looks like this:

graph: module {
  mo.graph @graph(%arg0: !mo.tensor<[1], f32>, %arg1: !mo.tensor<[1], f32>) -> !mo.tensor<[1], f32> no_inline {
    %0 = rmo.add(%arg0, %arg1) : !mo.tensor<[1], f32>, !mo.tensor<[1], f32>
    mo.output %0 : !mo.tensor<[1], f32>
  }
}

graph: module {
  mo.graph @graph(%arg0: !mo.tensor<[1], f32>, %arg1: !mo.tensor<[1], f32>) -> !mo.tensor<[1], f32> no_inline {
    %0 = rmo.add(%arg0, %arg1) : !mo.tensor<[1], f32>, !mo.tensor<[1], f32>
    mo.output %0 : !mo.tensor<[1], f32>
  }
}

To programmatically verify the complete graph construction, we use the graph.verify() method. This checks for various structural integrity criteria such as ensuring there are no cycles within the graph (acyclicity) which would indicate recursion or feedback loops that can not be part of the dataflow graph. For more details, check out the official documentation on the verify method.

2. Create inference session, load and compile the graph

With our graph now verified and ready, the next step involves creating an inference session instance, loading the graph into this session and compiling the graph into a model instance. We also print the input names to use when executing the model.

from max import engine

session = engine.InferenceSession()
model = session.load(graph)
print("input names are:")
for input_name in model.get_model_input_names():
    # Mojo lesson: `[]` dereferences in Mojo as `input_name` is of `Reference` type
    print(input_name[])

from max import engine

session = engine.InferenceSession()
model = session.load(graph)
print("input names are:")
for input_name in model.get_model_input_names():
    # Mojo lesson: `[]` dereferences in Mojo as `input_name` is of `Reference` type
    print(input_name[])

which outputs

input names are:
input0
input1

input names are:
input0
input1

Verifying input names input0 and input1 is crucial for correctly executing the model in the subsequent section.

3. Execute the graph/model with inputs

To execute the graph, we first create two input tensors in Mojo, specifying their names and values in the execute method. The result from the execution are returned as TensorMap, from which we can retrieve the value of output0 via the get method as follows

from tensor import Tensor

print("set some input values:")
input0 = Tensor[DType.float32](List[Float32](1.0))
print("input0:", input0)

input1 = Tensor[DType.float32](List[Float32](1.0))
print("input1:", input1)

print("obtain the result using `get`:")
# Mojo lesson: here the `^` in `input0^` passes the ownership and ends the lifetime of `input0`
ret = model.execute("input0", input0^, "input1", input1^)
print("result:", ret.get[DType.float32]("output0"))

from tensor import Tensor

print("set some input values:")
input0 = Tensor[DType.float32](List[Float32](1.0))
print("input0:", input0)

input1 = Tensor[DType.float32](List[Float32](1.0))
print("input1:", input1)

print("obtain the result using `get`:")
# Mojo lesson: here the `^` in `input0^` passes the ownership and ends the lifetime of `input0`
ret = model.execute("input0", input0^, "input1", input1^)
print("result:", ret.get[DType.float32]("output0"))

We can run the example code via magic run mojo add.mojo (the shorter version magic run add) and we can check the outputs are printed as follows

set some input values:
input0: Tensor([[1.0]], dtype=float32, shape=1)
input1: Tensor([[1.0]], dtype=float32, shape=1)
obtain the result using `get`:
result: Tensor([[2.0]], dtype=float32, shape=1)

set some input values:
input0: Tensor([[1.0]], dtype=float32, shape=1)
input1: Tensor([[1.0]], dtype=float32, shape=1)
obtain the result using `get`:
result: Tensor([[2.0]], dtype=float32, shape=1)

For more information, see the MAX Graph API example.

For a larger code example, check out our MAX Graph implementation of Llama2 and LLama3.

Now, let's explore our second example.

Build a matmul graph

In this example, we create a graph specifically for performing matrix multiplication (matmul) by a constant symbol which we will use further along in the next section. This type of graph is particularly important as it demonstrates how constant symbols, representing trained and fixed weights in a neural network, can be utilized. This concept will be expanded upon in subsequent sections.

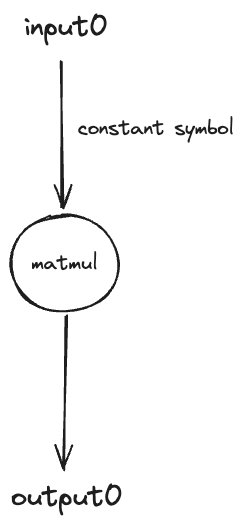
The setup for this matmul graph follows the same foundational steps as our initial example but includes some critical additions:

1. We introduce a symbolic dimension m to represent m x 2
2. The use graph.constant to create a constant symbol, crucial for maintaining static values

Here's how we compile and execute the graph to accommodate varying input tensor sizes at runtime:

from random import seed

from max.engine import InferenceSession
from max.graph import Graph, TensorType
from max.tensor import Tensor, TensorShape


def main():
    graph = Graph(TensorType(DType.float32, "m", 2))
    # create a constant tensor value to later create a graph constant symbol
    constant_value = Tensor[DType.float32](TensorShape(2, 2), 42.0)
    print("constant value:", constant_value)
    # create a constant symbol
    constant_symbol = graph.constant(constant_value)
    # create a matmul node
    mm = graph[0] @ constant_symbol
    graph.output(mm)
    # verify
    graph.verify()

    # create session, load and compile the graph
    session = InferenceSession()
    model = session.load(graph)

    # generate random input
    seed(42)
    input0 = Tensor[DType.float32].randn((2, 2))
    print("random 2x2 input0:", input0)
    ret = model.execute("input0", input0^)
    print("matmul 2x2 result:", ret.get[DType.float32]("output0"))

    # with 3 x 2 matrix input
    input0 = Tensor[DType.float32].randn((3, 2))
    print("random 3x2 input0:", input0)
    ret = model.execute("input0", input0^)
    print("matmul 3x2 result:", ret.get[DType.float32]("output0"))

from random import seed

from max.engine import InferenceSession
from max.graph import Graph, TensorType
from max.tensor import Tensor, TensorShape


def main():
    graph = Graph(TensorType(DType.float32, "m", 2))
    # create a constant tensor value to later create a graph constant symbol
    constant_value = Tensor[DType.float32](TensorShape(2, 2), 42.0)
    print("constant value:", constant_value)
    # create a constant symbol
    constant_symbol = graph.constant(constant_value)
    # create a matmul node
    mm = graph[0] @ constant_symbol
    graph.output(mm)
    # verify
    graph.verify()

    # create session, load and compile the graph
    session = InferenceSession()
    model = session.load(graph)

    # generate random input
    seed(42)
    input0 = Tensor[DType.float32].randn((2, 2))
    print("random 2x2 input0:", input0)
    ret = model.execute("input0", input0^)
    print("matmul 2x2 result:", ret.get[DType.float32]("output0"))

    # with 3 x 2 matrix input
    input0 = Tensor[DType.float32].randn((3, 2))
    print("random 3x2 input0:", input0)
    ret = model.execute("input0", input0^)
    print("matmul 3x2 result:", ret.get[DType.float32]("output0"))

Here are the results of matmul graph using a constant symbol of 2 x 2 tensor and a random input tensors of shapes 2 x 2 or 3 x 2 for demonstration.

We can run the code via magic run mojo matmul.mojo

constant value: Tensor([[42.0, 42.0],
[42.0, 42.0]], dtype=float32, shape=2x2)

random 2x2 input0: Tensor([[2.1224555969238281, -1.5332902669906616],
[-0.11786748468875885, 1.3148393630981445]], dtype=float32, shape=2x2)
matmul 2x2 result: Tensor([[24.744943618774414, 24.744943618774414],
[50.272819519042969, 50.272819519042969]], dtype=float32, shape=2x2)
random 3x2 input0: Tensor([[0.92314141988754272, -0.10077553242444992],
[-1.7947894334793091, 0.42195448279380798],
[-1.2157822847366333, -0.062963984906673431]], dtype=float32, shape=3x2)
matmul 3x2 result: Tensor([[34.53936767578125, 34.53936767578125],
[-57.659069061279297, -57.659069061279297],
[-53.707344055175781, -53.707344055175781]], dtype=float32, shape=3x2)

constant value: Tensor([[42.0, 42.0],
[42.0, 42.0]], dtype=float32, shape=2x2)

random 2x2 input0: Tensor([[2.1224555969238281, -1.5332902669906616],
[-0.11786748468875885, 1.3148393630981445]], dtype=float32, shape=2x2)
matmul 2x2 result: Tensor([[24.744943618774414, 24.744943618774414],
[50.272819519042969, 50.272819519042969]], dtype=float32, shape=2x2)
random 3x2 input0: Tensor([[0.92314141988754272, -0.10077553242444992],
[-1.7947894334793091, 0.42195448279380798],
[-1.2157822847366333, -0.062963984906673431]], dtype=float32, shape=3x2)
matmul 3x2 result: Tensor([[34.53936767578125, 34.53936767578125],
[-57.659069061279297, -57.659069061279297],
[-53.707344055175781, -53.707344055175781]], dtype=float32, shape=3x2)

With this foundation, we are ready to explore more advanced applications in the next section of the tutorial.

Build an MNIST classifier graph

In this section, we demonstrate how to build a two-layer neural network with ReLU activation using PyTorch, train it on the famous MNIST data featuring black and white 28 x 28 pixel images of handwritten digits (0 to 9 i.e. total of 10 classes) and then test its accuracy.

Subsequently, we will implement the same model using the MAX Graph API for inference to ensure the accuracy remains consistent.

1. Build and train the model in PyTorch

First, to set up, let's define our neural network in PyTorch:

import torch.nn as nn

class Model(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super().__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, num_classes)

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

import torch.nn as nn

class Model(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super().__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, num_classes)

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

We can train and test the network as follows (python mnist.py)

loss_fn = nn.CrossEntropyLoss()
optimizer = optim.RMSprop(model.parameters(), lr=learning_rate)
total_steps = len(train_loader)
for epoch in range(num_epochs):
    for i, (images, labels) in enumerate(train_loader):
        images = images.reshape(-1, 28 * 28)
        outputs = model(images)
        loss = loss_fn(outputs, labels)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if (i+1) % 100 == 0:
            print (f'Epoch [{epoch+1}/{num_epochs}], Step [{i+1}/{total_steps}], Loss: {loss.item():.4f}')

# test
model.eval()
with torch.no_grad():
    correct = 0
    total = 0
    for images, labels in test_loader:
        images = images.reshape(-1, 28 * 28)
        outputs = model(images)
        probs = F.softmax(outputs, dim=1)
        predicted = torch.argmax(probs, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

    print(f"Accuracy of the network on the 10000 test images: {100 * correct / total} %")

# save weights in numpy binary format
weights = {}
for name, param in model.named_parameters():
    weights[name] = param.detach().cpu().numpy()

np.save(f"model_weights.npy", weights)

loss_fn = nn.CrossEntropyLoss()
optimizer = optim.RMSprop(model.parameters(), lr=learning_rate)
total_steps = len(train_loader)
for epoch in range(num_epochs):
    for i, (images, labels) in enumerate(train_loader):
        images = images.reshape(-1, 28 * 28)
        outputs = model(images)
        loss = loss_fn(outputs, labels)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if (i+1) % 100 == 0:
            print (f'Epoch [{epoch+1}/{num_epochs}], Step [{i+1}/{total_steps}], Loss: {loss.item():.4f}')

# test
model.eval()
with torch.no_grad():
    correct = 0
    total = 0
    for images, labels in test_loader:
        images = images.reshape(-1, 28 * 28)
        outputs = model(images)
        probs = F.softmax(outputs, dim=1)
        predicted = torch.argmax(probs, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

    print(f"Accuracy of the network on the 10000 test images: {100 * correct / total} %")

# save weights in numpy binary format
weights = {}
for name, param in model.named_parameters():
    weights[name] = param.detach().cpu().numpy()

np.save(f"model_weights.npy", weights)

After training and testing the network, we found the model achieves an accuracy of 97.03% on the test dataset.

Run the code via magic run python mnist.py

Epoch [1/5], Step [100/469], Loss: 0.5389
Epoch [1/5], Step [200/469], Loss: 0.2278
Epoch [1/5], Step [300/469], Loss: 0.3192
Epoch [1/5], Step [400/469], Loss: 0.2647
Epoch [2/5], Step [100/469], Loss: 0.1070
Epoch [2/5], Step [200/469], Loss: 0.2188
Epoch [2/5], Step [300/469], Loss: 0.2354
Epoch [2/5], Step [400/469], Loss: 0.1564
Epoch [3/5], Step [100/469], Loss: 0.1239
Epoch [3/5], Step [200/469], Loss: 0.1318
Epoch [3/5], Step [300/469], Loss: 0.0660
Epoch [3/5], Step [400/469], Loss: 0.1235
Epoch [4/5], Step [100/469], Loss: 0.0650
Epoch [4/5], Step [200/469], Loss: 0.0683
Epoch [4/5], Step [300/469], Loss: 0.1512
Epoch [4/5], Step [400/469], Loss: 0.1213
Epoch [5/5], Step [100/469], Loss: 0.0192
Epoch [5/5], Step [200/469], Loss: 0.0286
Epoch [5/5], Step [300/469], Loss: 0.1031
Epoch [5/5], Step [400/469], Loss: 0.0407
Accuracy of the network on the 10000 test images: 97.03 %

Epoch [1/5], Step [100/469], Loss: 0.5389
Epoch [1/5], Step [200/469], Loss: 0.2278
Epoch [1/5], Step [300/469], Loss: 0.3192
Epoch [1/5], Step [400/469], Loss: 0.2647
Epoch [2/5], Step [100/469], Loss: 0.1070
Epoch [2/5], Step [200/469], Loss: 0.2188
Epoch [2/5], Step [300/469], Loss: 0.2354
Epoch [2/5], Step [400/469], Loss: 0.1564
Epoch [3/5], Step [100/469], Loss: 0.1239
Epoch [3/5], Step [200/469], Loss: 0.1318
Epoch [3/5], Step [300/469], Loss: 0.0660
Epoch [3/5], Step [400/469], Loss: 0.1235
Epoch [4/5], Step [100/469], Loss: 0.0650
Epoch [4/5], Step [200/469], Loss: 0.0683
Epoch [4/5], Step [300/469], Loss: 0.1512
Epoch [4/5], Step [400/469], Loss: 0.1213
Epoch [5/5], Step [100/469], Loss: 0.0192
Epoch [5/5], Step [200/469], Loss: 0.0286
Epoch [5/5], Step [300/469], Loss: 0.1031
Epoch [5/5], Step [400/469], Loss: 0.0407
Accuracy of the network on the 10000 test images: 97.03 %

Next, we implement the PyTorch model in MAX Graph API for inference.

2. Build the inference graph with MAX Graph

After training our model and saving its weights, we need to construct an inference graph and load the weights as constant symbols. Our graph will handle input dimensions with a symbolic "batch" dimension and static 28x28 spatial dimensions, representing flattened and preprocessed images. We will also include a softmax operation via ops.softmax to compute probabilities directly within the inference graph.

from max.graph import Graph, TensorType, ops
from max import engine

def build_mnist_graph(
    fc1w: Tensor[DType.float32],
    fc1b: Tensor[DType.float32],
    fc2w: Tensor[DType.float32],
    fc2b: Tensor[DType.float32],
    ) -> Graph:
    # Note: "batch" is a symbolic dim which is known ahead of time vs dynamic dim
    graph = Graph(TensorType(DType.float32, "batch", 28 * 28))
    # PyTorch linear is defined as: x W^T + b so we need to transpose the weights
    fc1 = (graph[0] @ ops.transpose(graph.constant(fc1w), 1, 0)) + graph.constant(fc1b)
    relu = ops.relu(fc1)
    fc2 = (relu @ ops.transpose(graph.constant(fc2w), 1, 0)) + graph.constant(fc2b)
    out = ops.softmax(fc2) # adding explicit softmax for inference prob
    graph.output(out)
    graph.verify()
    return graph

from max.graph import Graph, TensorType, ops
from max import engine

def build_mnist_graph(
    fc1w: Tensor[DType.float32],
    fc1b: Tensor[DType.float32],
    fc2w: Tensor[DType.float32],
    fc2b: Tensor[DType.float32],
    ) -> Graph:
    # Note: "batch" is a symbolic dim which is known ahead of time vs dynamic dim
    graph = Graph(TensorType(DType.float32, "batch", 28 * 28))
    # PyTorch linear is defined as: x W^T + b so we need to transpose the weights
    fc1 = (graph[0] @ ops.transpose(graph.constant(fc1w), 1, 0)) + graph.constant(fc1b)
    relu = ops.relu(fc1)
    fc2 = (relu @ ops.transpose(graph.constant(fc2w), 1, 0)) + graph.constant(fc2b)
    out = ops.softmax(fc2) # adding explicit softmax for inference prob
    graph.output(out)
    graph.verify()
    return graph

With the inference graph defined, we can now execute it with test images.

3. Run inference and check accuracy

To execute the graph, we first convert the model weights from numpy format to Mojo tensor format, then create the graph, compile it, and run inference. Finally, to check the accuracy, we iterate on test images, preprocess them, obtain the result and calls argmax to find the predicted value between the 10 classes and count how many of them correctly match the ground truth label.

weights_dict = load_model_weights()
fc1w = numpy_to_tensor[DType.float32](weights_dict["fc1.weight"])
fc1b = numpy_to_tensor[DType.float32](weights_dict["fc1.bias"])
fc2w = numpy_to_tensor[DType.float32](weights_dict["fc2.weight"])
fc2b = numpy_to_tensor[DType.float32](weights_dict["fc2.bias"])

mnist_graph = build_mnist_graph(fc1w^, fc1b^, fc2w^, fc2b^)
session = engine.InferenceSession()
model = session.load(mnist_graph)

correct = 0
total = 0
# use batch size of 1 in this example
test_dataset = load_mnist_test_data()
for i in range(len(test_dataset)):
    item = test_dataset[i]
    image = item[0]
    label = item[1]

    preprocessed_image = preprocess(image)

    output = model.execute("input0", preprocessed_image)
    probs = output.get[DType.float32]("output0")

    predicted = probs.argmax(axis=1)

    label_ = Tensor[DType.index](TensorShape(1), int(label))
    correct += int(predicted == label_)
    total += 1

print("Accuracy of the network on the 10000 test images:", 100 * correct / total, "%")

weights_dict = load_model_weights()
fc1w = numpy_to_tensor[DType.float32](weights_dict["fc1.weight"])
fc1b = numpy_to_tensor[DType.float32](weights_dict["fc1.bias"])
fc2w = numpy_to_tensor[DType.float32](weights_dict["fc2.weight"])
fc2b = numpy_to_tensor[DType.float32](weights_dict["fc2.bias"])

mnist_graph = build_mnist_graph(fc1w^, fc1b^, fc2w^, fc2b^)
session = engine.InferenceSession()
model = session.load(mnist_graph)

correct = 0
total = 0
# use batch size of 1 in this example
test_dataset = load_mnist_test_data()
for i in range(len(test_dataset)):
    item = test_dataset[i]
    image = item[0]
    label = item[1]

    preprocessed_image = preprocess(image)

    output = model.execute("input0", preprocessed_image)
    probs = output.get[DType.float32]("output0")

    predicted = probs.argmax(axis=1)

    label_ = Tensor[DType.index](TensorShape(1), int(label))
    correct += int(predicted == label_)
    total += 1

print("Accuracy of the network on the 10000 test images:", 100 * correct / total, "%")

The output of magic run mojo mnist.mojo is

Accuracy of the network on the 10000 test images: 97.030000000000001 %

Accuracy of the network on the 10000 test images: 97.030000000000001 %

This matches the accuracy we observed from the PyTorch test, confirming that our MAX Graph API implementation performs equivalently.

Next steps

In this tutorial, we demonstrated how to use MAX Graph API step-by-step, to create a symbolic graph, compile and execute such graphs. We also showed how to replicate a two layer neural network trained in PyTorch, in MAX Graph API and saw that the test accuracy remained intact. We hope that by the end of this tutorial, you have gained a better understanding of the inner workings of MAX Graph APIs.

Here are a few potential steps for you:

• Explore other neural network architectures beyond a simple two-layer feed-forward network and implement them using MAX Graph API
• Test and assess correctness and contribute to the community 🚀

Report feedback, including issues on our Mojo and MAX GitHub tracker.

Did this tutorial work for you?

Thank you! We'll create more content like this.

Thank you for helping us improve!

😔 What went wrong?

Some code doesn’t work

It's missing a step; I don't know what to do

I don't understand the purpose

Other

Submit